Invariant moments

Computing the moments of invariant is a way to recognize the visual patterns and characters independent on its position, size and orientation[1-2].

The moments of invariant of images were computed in this activity. We have a set of images which consists of the original image, rotated image and scaled image. Consider first a set of grayscale images as shown below.

Set of grayscale images. Original image, rotated image, and scaled image (from left to right) . 

The 2D moment of order (p+q) of an image was given by
$$m_{pq} = \sum_{x=0}^{N-1} \sum_{y=0}^{M-1} x^p y^q f(x,y)$$
The central moment is then given by
$$\mu_{pq} = \sum_{x=0}^{N-1} \sum_{y=0}^{M-1} (x-\bar{x})^p (y-\bar{y})^q f(x,y)$$
where $\bar{x}$ and $\bar{y}$ are calculated using the following equations
$$\bar{x} = \frac{m_{10}}{m_{00}}; \bar{y} = \frac{m_{01}}{m_{00}}$$
The normalized central moments $\eta_{pq}$ is now computed as
$$\eta_{pq} = \frac{\mu_{pq}}{\mu_{00}^\gamma}; \gamma = \frac{p+q}{2} +1$$

From the second and third order of moments, a set of seven invariant moments was derived.

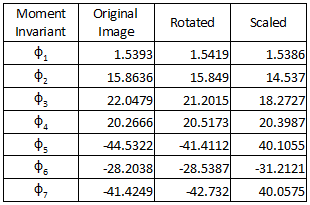
In matlab, the computation is done using for loop to access each pixel position and the value of the image in that position. The calculated invariant moments for the grayscale image set are summarized in the table below. For each invariant moment, the values are nearly the same for the three images. The closely similar values of the invariant moments just justifies that the images are recognized to have the same pattern regardless of the rotation and the size.

The same procedure was done for other set of images. Unlike the grayscale images which have an image function $f$ that ranges from 0 to 255, the succeeding sets of images are binary images which have values that are only either 0 or 1. Edge images are like Dirac delta function which has peak values (equal to 1) located at the edge otherwise, the values were zero. 

I applied the same procedure first for my chromosome edge image in the last activity but the resulting invariant moment values were not that similar to each other. When discussing with Anjali, she thought that maybe there were too little details that this approach wasn't able to recognize the patterns. So I tried other edge image that have a many details as shown in the figure below. 

The values of the moments invariant for the set of edge image are tabulated below. Now, the values for each moment invariant were observed to be closely similar. And since the edge images are mostly zeros in values, the invariant moment values are also smaller as compared to that of the grayscale set of images. The eight invariant moments for this set is just in the range of [0.2, 7.4].

Lastly, the moments invariants for the set of synthetic symmetric images were also computed. They were like step function which have zero values for the background, then they have values of ones when they pass through the boundary of their shape. You may refer to the figure below.

Again, I just first tried the method for simple images but they resulted to not so similar vaules. Also, this computation of invariant moments by Hu tends to be sensitive to symmetry. That's why another way of computing moment invariant that considers symmetry was studied by Flusser and Suk[2]. Table below shows the invariant moments for the set of edge images. There are only nice results for the first three moments but the rest have relativity not similar values.

So again,  I choose a more detailed set of images and their invariant moments resulted to closely equal values. The set of more detailed symmetric synthetic images and their corresponding moment invariants are shown below.

---

Reference

[1] Hu, Ming-Kuei. "Visual pattern recognition by moment invariants." Information Theory, IRE Transactions on 8.2 (1962): 179-187.
[2] Flusser, Jan, and Tomás Suk. "Rotation moment invariants for recognition of symmetric objects." IEEE Transactions on Image Processing 15.12 (2006): 3784-3790.
[3] Gonzalez, Rafael C. Digital image processing. Chapter 11, Pearson Education India, 2009.